1. INTRODUCTION
The amount of computation required for neural network language models mainly lies in their output layers in which the number of nodes is equal to the size of vocabulary, usually several ten thousands. If the size of output layer can be reduced, the amount of computation will decreased. The idea of word classes was first invested for neural network language modeling by Mikolov et al. (2011) to solve this problem. With word classes, every word in vocabulary is assigned to a unique class, and the conditional probability of a word given its history can be decomposed into the probability of the word’s class given its history and the probability of the word given its class and history, this is:
where $c(w_t)$ is the class of word $w_t$. The architecture of class based LSTM-RNNLM is illustrated in Figure 1, and $p$, $q$ are the lower and upper index of words in a class respectively.
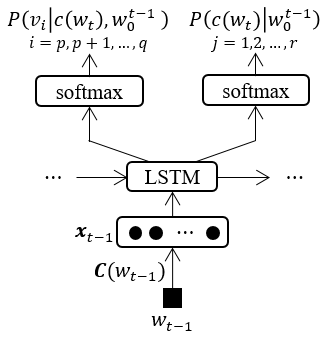
Figure 1. Architecture of class based LSTM-NNLM
Before Mikolov et al. (2011), Morin and Bengio (2005) extended word classes to a hierarchical binary clustering of words and built a hierarchical neural network language model. In hierarchical neural network language model, instead of assigning every word in vocabulary with a unique class, a hierarchical binary tree of words is built according to the word similarity information extracted from WordNet (C. Fellbaum, 1998), and every word in vocabulary is assigned with a bit vector:
When $b_{1}(v_i),b_{2}(v_i),\dots,b_{j-1}(v_i)$ are given, $b_j(v_i)=0, j=1,2,\dots,l$ indicates that word $v_i$ belongs to the sub-group 0 of current node and $b_j(v_i)=1$ indicates it belongs to the other one. The conditional probability of every word is represented as:
2. ALGORITHMS FOR CLASS ASSIGNMENT
The simple way to assign word classes is to cluster words uniformly and randomly. Mikolov et al. (2011) proposed two algorithms to classify words according to their frequencies in training data set. When building vocabulary from training data set, the frequency of each word in training data set is counted. The sum of all words’ frequenies is:
where, is the size of vocabulary, is the frequency of each word. Before classifing words into classed, all the words are sorted in descend order according to their frequencies. Then assign class index to words one by one according to the accumulation probabilty of each word. For the th word, it will be classified into th class if its accumulation probability satisfies the following criterion:
where is the total number of word classes whose optimal value is around .
This algorithm is optimized further by clustering words using sqrt frequency:
For the th word, it will be classified into word class if its accumulation square probability satisfies the following condition:
3. COMPARISON OF DIFFERENT ALGORITHM
Theoretically, an exponential speed-up, on the order of $k/\textrm{log}_{2}k$, can be achieved with this hierarchical architecture. In Morin and Bengio (2005), impressive speed-up during both training and test, which were less than the theoretical one, were obtained but an obvious increase in PPL was also observed. One possible explanation for this phenomenon is that the introduction of hierarchical architecture or word classes impose negative influence on the word classification by neural network language models. As is well known, a distribution representation for words, which can be used to represent the similarities between words, is formed by neural network language models during training. When words are clustered into classes, the similarities between words from different classes cannot be recognized directly. For a hierarchical clustering of words, words are clustered more finely which might lead to worse performance, i.e., higher perplexity, and deeper the hierarchical architecture is, worse the performance would be.
To explore this point further, hierarchical LSTM-NNLMs with different number of hierarchical layers were built. In these hierarchical LSTM-NNLMs, words were clustered randomly and uniformly instead of according to any word similarity information. The results of experiment on these models are showed in Table 1 which strongly support the above hypothesis. When words are clustered into hierarchical word classes, the speed of both training and test increase, but the effect of speed-up decreases and the performance declines dramatically as the number of hierarchical layers increases. Lower perplexity can be expected if some similarity information of words is used when clustering words into classes. However, because of the ambiguity of words, the degradation of performance is unavoidable by assigning every word with a unique class or path. On the other hand, the similarities among words recognized by neural network is hard to defined, but it is sure that they are not confined to linguistical ones.
Table 1. Results for class-based models
| Models | $m$ | $n_h$ | Method | $l$ | PPL | Train(words/s) | Test(words/s) |
|---|---|---|---|---|---|---|---|
| LSTM-NNLM | 200 | 200 | Uniform | 1 | 227.51 | 607.09 | 2798.97 |
| LSTM-NNLM | 15 | 200 | Uniform | 3 | 312.82 | 683.04 | 3704.28 |
| LSTM-NNLM | 6 | 200 | Uniform | 5 | 438.58 | 694.43 | 3520.27 |
| LSTM-NNLM | 200 | 200 | Freq | 1 | 248.99 | 600.56 | 2507.97 |
| LSTM-NNLM | 200 | 200 | Sqrt-Freq | 1 | 237.93 | 650.16 | 3057.27 |
The experiment results (Table 1) indicate that higher perplexity and a little more training time were obtained when the words in vocabulary were classified according to their frequencies than classified randomly and uniformly. When words are clustered into word classed using their frequency, words with high frequency, which contribute more to final perplexity, are clustered into very small word classes, and this leads to higher perplexity. On the other hand, word classes consist of words with low frequency are much bigger which causes more training time. However, as the experiment results show, both perplexity and training time were improved when words were classified according to their sqrt frequency, because word classes were more uniform when built in this way. All other models in this paper were speeded up using word classes, and words were clustered according to their sqrt frequencies.



